|
us & holo-links
Who to contact about what...
theories: spacermike00@yahoo.ca
Black Holes and Neutron Stars
The Main Point
Studying neutron stars and black holes gives us access to exotic realms that we can't explore on Earth.
Abstract
Neutron stars and black holes are among the most exotic objects in the universe. A lump of neutron star matter the size
of a sugar cube would weigh as much as all humanity, and the stars have magnetic fields a trillion times Earth's. Since we
can't reproduce such conditions in laboratories, we have to observe neutron stars with telescopes to figure out their properties.
Recently the Rossi Explorer, a new X-ray satellite, discovered a remarkable new phenomenon of neutron stars that strip matter
from their companion stars: their brightness varies almost periodically more than a thousand times per second. I will describe
how this phenomenon gives us a sensitive new tool to probe the properties of neutron stars, and how it may even help us search
for black holes.
Intro to Black Holes
A black hole is a region of space in which the matter is so compact that nothing can escape from it, not even
light; the "surface" of a black hole, inside of which nothing can escape, is called an event horizon. The matter
that forms a black hole is crushed out of existence. Just as the Cheshire Cat disappeared and left only its smile behind,
a black hole represents matter that leaves only its gravity behind.
Black holes are usually formed when an extremely massive star dies in a supernova. However, some people think small black
holes were formed during the Big Bang, and that the resulting "mini black holes" may be in great abundance in our galaxy.
In principle, black holes can have any mass; black holes formed by stellar death have at least twice the mass of our Sun.
Unlike ordinary things (e.g., rocks), which have a size roughly proportional to the cube root of their mass, black holes have
radii proportional to their mass. The event horizon of a nonrotating black hole the mass of our Sun has a radius about 3~km.
Thus, large black holes aren't very dense! A black hole a billion times as massive as our Sun, such as is thought to exist
in the center of some galaxies, has an average density just twenty times the density of air.
Black holes, like any gravitating objects, exert a tidal force. If you approach a black hole feet first, the gravitational
force at your feet is greater than the force at your head. The tidal force at the event horizon is smaller for larger black
holes: you would get torn to shreds far outside a black hole the mass of our sun, but at the event horizon of a billion solar
mass black hole the tidal force would only be a millionth of an ounce!
Strange Facts About Black Holes
- Light bends so much near black holes that if you were near one and looking away from the hole, you would see multiple
images of every star in the universe, and could actually see the back of your own head!
- Inside a black hole the roles of time and radius reverse: just as now you can't avoid going into the future, inside a
black hole you can't avoid going in to the central singularity.
- If you stood a safe distance from a black hole and saw a friend fall in, he would appear to slow down and almost stop
just outside the event horizon. His image would dim very rapidly. Unfortunately for him, from his point of view he would cross
the event horizon just fine, and would meet his doom at the singularity.
- Black holes are the simplest objects in the universe. You can describe one completely by just its mass, spin rate, and
electric charge. In contrast, to completely describe a dust mote you're have to specify the position and state of all of its
atoms, taking at least $10^{16}$ numbers!
- As Hawking discovered, black holes can evaporate, but only very slowly. Even one the mass of a mountain will last for
ten billion years, and one the mass of the Sun will only evaporate after $10^{67}$ years.
How Do We Detect Black Holes?Black holes don't radiate light, and an object that falls inside a black hole
doesn't emit light either, so detecting them can be challenging.
Just as with neutron stars, if a black hole is in a binary and it strips gas from its companion, we can detect X-rays from
the resulting accretion disk (see "Observing Neutron Stars"). The light from accretion disks around black holes looks very similar to the light from disks around neutron stars,
and it is not always possible to tell with certainty which object lurks at the center of the disk, although in six cases so
far we're sure that the central object is a black hole.
You can also infer the presence of a black hole in the center of some galaxies. This is done by observing stars near the
center of the galaxy. If the stars are moving very rapidly around some unseen object, Kepler's laws can be used to estimate
the mass in the center. In some cases the mass must be at least a hundred million times our Sun's mass, in a region only a
few light years across. Astronomers are virtually certain that the only explanation is a black hole, but we lack direct evidence.
The detection of black holes is very difficult and controversial, and it is being studied actively by many research groups.
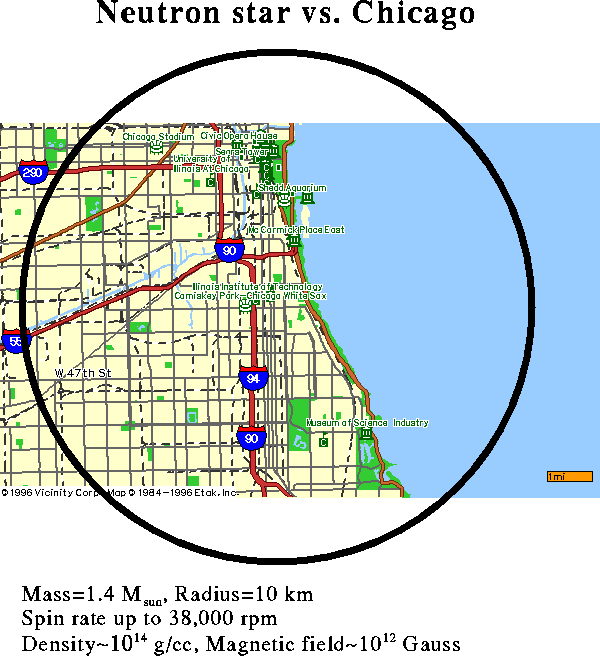
Origin and Scale of Neutron StarsA neutron star has roughly the mass of our Sun crammed in a ball ten kilometers
in radius. Its density is therefore a hundred trillion times the density of water; at that density, all the people on Earth
could be fit into a teaspoon! Neutron stars are born during supernova, and are held up by neutron degeneracy pressure.
These stars are relatively rare: only about 10^8 in our galaxy, or one in a thousand stars, so the nearest one is probably
at least 40 light years away.
Neutron Stars and Extreme Physics
- Density at center can be several times the density of an atomic nucleus, so we can't explore this regime in laboratories.
The properties of this matter are unknown, and may include such exotic things as enormous conglomerations of quarks.
- Magnetic fields are a trillion times Earth's, and more than a million times as strong as can be achieved in laboratories.
- Matter in the central parts of neutron stars is thought to be a superconductor, even at a hundred million degrees!
Neutron
stars therefore have states of matter that cannot be duplicated in laboratories. Study of them helps us test our theories,
and perhaps discover new physics. But how can we observe neutron stars?
Observing Neutron Stars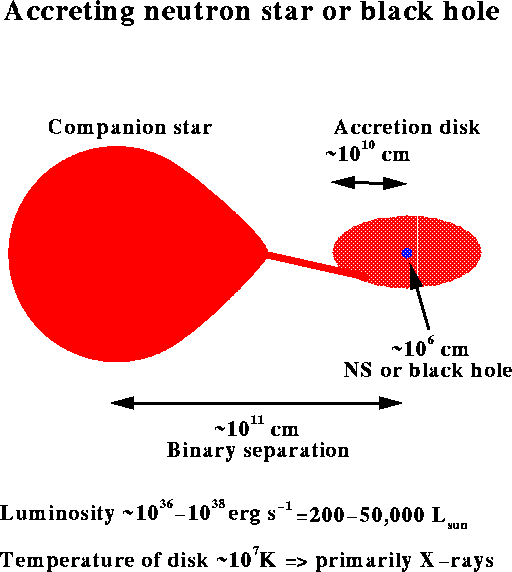
We see a normal star by the light it gives off during fusion. Neutron stars are very hot, more than 100,000 K for most
of their lifetimes, so this sounds promising but most of the energy comes out as X-rays (not visible light). Also, neutron
stars are so small that at typical distances they are ten billion times fainter than you can see with your naked eye, which
is too faint for even the Hubble Space Telescope. We need some other way to see neutron stars.
One way is to see them as radio pulsars. Another way is if the neutron star is one member of a binary, in which case the
gravity of the neutron star can strip gas off its companion. The gas from the companion falls onto the neutron star, and emits
fantastic power in X-rays: as much as 50,000 times the luminosity the Sun produces. This is a tremendously efficient way to
generate energy. Dropping a kilogram of matter onto the surface of a neutron star releases as much energy as a five megaton
hydrogen bomb!
Since the neutron star is a very small target, astronomically speaking, gas can't fall onto it directly. Instead, gas spirals
around the neutron star, and friction with itself releases huge amounts of energy in what is called an accretion disk.
Studying the X-rays from accretion disks can give us hints about the star: for example, how does matter behave at extremely
high densities?
The Equation of StateAs mentioned above, we want to know the properties of the extremely dense matter in
the center of neutron stars. One way to characterize the matter is by its equation of state.
The equation of state can be pictured as the relation between the density of matter and its pressure. Consider a glass
of water. The shape of the water in the glass can be changed easily (e.g., by sloshing it around), but the volume, and hence
the density, of the water is extremely difficult to change. Even if you apply a huge amount of pressure to the water, for
example by a piston, the density changes hardly at all; this is the basis of hydraulic presses. Water may therefore be said
to have a stiff equation of state. In contrast, the volume of air in an empty glass can be changed easily, with little
pressure, so air may be said to have a soft equation of state. So, a knowledge of the equation of state tells us,
essentially, how squeezable the matter is.
In the case of a neutron star, knowledge of both the mass and radius of a particular neutron star would tell us the equation
of state. This is because gravity squeezes the star, and the more mass the star has the more gravity squeezes it. If the star
has a large radius (meaning, say, 15~km!), it was relatively successful in resisting gravity and thus has a very stiff equation
of state. If the star has a small radius (say, 8~km), it was not as successful in resisting gravity and it has a softer equation
of state. We therefore need to estimate the mass and radius of neutron stars.
Estimating NS Masses and RadiiNo easy task, this. Astronomical measurements are often challenging, because
we can't go to a star and experiment on it. Neutron stars are especially tough, because they are relatively small and far
away: even the closest one would appear to be the size of a bacterium on the Moon, so we have to find other ways to determine
the mass or radius of a neutron star.
One way to do this is to use Kepler's laws. If we can figure out how far two stars in a binary are from each other, and
the duration of their orbital period, we know something about their masses. Only for neutron stars in binaries do we have
even a rough estimate of the mass, and in only a few of those cases do we know the mass accurately.
Estimating the radius is much more difficult than estimating the mass. Unlike the mass, the radius doesn't have any strong
effects on what we can observe. From astronomical observations alone, neutron stars could have radii from 5~km to 30~km (although
most of that range, all but about 7~km to 20~km, is ruled out by what we know of nuclear physics).
So, we need some kind of breakthrough in the evidence to allow us to further constrain the radii of neutron stars.
An Unexpected DiscoveryWe can only discover what our instruments can detect, so many times in astrophysics
a breakthrough in our understanding has come from an improvement in instrumental capabilities.
Such was the case when the Rossi X-ray Timing Explorer was launched on December 30, 1995. Its many outstanding
properties include an unprecedented sensitivity to very rapid variations of the X-ray intensity of accreting neutron stars,
i.e., neutron stars stripping mass from their stellar companions. This led to the discovery of a completely unexpected phenomenon:
fast intensity oscillations, sometimes more than a thousand times per second!
Kilohertz Intensity OscillationsFigure 1 shows the X-ray brightness from one neutron star system, as a function of time. The intensity goes up and down nearly 1000
times per second. There are at least 10 known neutron stars that show this, and we have discovered that:
- The intensity variations are fast, up to 1200 times per second
- For a given neutron star, the frequency of the variations goes up and down with time: in one case, the variation can be
anywhere from 500 per second to 1100 per second
The dramatic change in frequency means that it can't be something
simple like the spin frequency of the neutron star, since the star can't easily be spun up or down. However, the common occurrence
of this phenomenon and its other properties mean that it is telling us something fundamental about the flow of matter onto
neutron stars.
Click to see my proposed explanation of this phenomenon.
Implications
- The frequency with which the clump goes around the star is calculated by Kepler's laws: the higher the frequency, the
closer the clump has to be to the star. This limits the radius of the star.
- When the effects of Einstein's general relativity are included, it turns out that we also get an upper limit to the mass
of the star.
- The result is that the neutron stars in these systems must have masses less than 2.2 times our Sun's mass, and radii less
than 17~km. This is the first convincing observational limit to the radius of neutron stars.
Key Points
- The matter in the center of neutron stars is incredibly dense, and we can't reproduce it on Earth.
- So, the study of neutron stars can tell us things about the universe that would otherwise remain forever undiscovered.
- One way to find out about the dense matter of neutron stars is to determine the equation of state of neutron stars, which
is the relation between their pressure and density.
- The equation of state is known if we know both the mass and radius of a neutron star.
- But, astronomical observations are indirect: we can't experiment on stars.
- Neutron stars are particularly difficult, since they are relatively small and distant.
- Luckily for us, the recently-discovered phenomenon of rapid X-ray intensity oscillations may allow us, for the first time,
to estimate both the mass and radius of some neutron stars and thus know their equation of state.
- As it turns out, if we knew the equation of state of neutron stars, we would also know their maximum mass. This ends up
helping in the search for black holes in our galaxy.
- This phenomenon is still new, and we continue to learn things about it at a rapid pace, both observationally and theoretically;
these are exciting times!
Glossary
- Accretion disk:
- the pattern of flow of matter from a normal star to a neutron star or black hole, which is flattened and thus disk-like.
- Degeneracy pressure:
- a quantum-mechanical phenomenon; fermions, such as electrons or neutrons, obey Pauli's exclusion principle, so that no
two fermions can occupy the same state. Thus, if fermions are squeezed together they resist even if there is no temperature
and no energy generation. This resistance to squeezing is degeneracy pressure.
- Equation of state:
- the relation between the pressure and density of a given type of matter, which is an indication of how the matter resists
squeezing. If the matter resists squeezing strongly (e.g., water), the equation of state is stiff; if it resists
squeezing only weakly (e.g., air), the equation of state is soft.
- Event horizon:
- in a black hole, the point beyond which events cannot be detected. This is the point of no return; an object that falls
inside the event horizon can't get out.
- Kepler's laws:
- rules for the orbital motion of planets or anything else bound by gravity. The law of most interest here is that the square
of the orbital period is proportional to the cube of the orbital separation, and inversely proportional to the mass. Thus,
if we see an orbital period, we can estimate the mass or orbital separation and therefore constrain the mass and radius of
a neutron star.
- Singularity:
- in a black hole, the "center point", at which densities, tidal forces, and other physical quantities become infinite.
Our current physical theories break down at this point.
- Tidal force:
- the force an object feels because of the differential pull of gravity at different distances.
Related Web Resources
- http://jovian.physics.uoguelph.ca/~droz/inside/
- Black Holes:The inside story. Includes lots of diagrams and suggestions for further reading. The explanations are thorough
and very readable.
- http://www.astro.umd.edu/~miller/nstar.html
- Moderately technical guide to various aspects of neutron star physics
- http://antwrp.gsfc.nasa.gov/htmltest/rjn_bht.html
- Robert Nemiroff's page on virtual trips to black holes and neutron stars. Neat animation showing gravitational light bending!
- http://physics7.berkeley.edu/BHfaq.html
- Black hole FAQ at Berkeley. Accurate, yet accessible
So, like, how do we get neutron stars?
Neutron stars are believed to form in supernovae such as the one that formed the Crab Nebula (or check out this cool X-ray image of the nebula, from the Chandra X-ray Observatory). The stars that eventually become neutron stars are thought to start out
with about 15 to 30 times the mass of our sun. These numbers are probably going to change as supernova simulations become
more precise, but it appears that for initial masses much less than 15 solar masses the star becomes a white dwarf, whereas
for initial masses a lot higher than 30 solar masses you get a black hole instead (this may have happened with Supernova 1987A, although detection of neutrinos in the first few seconds of the supernova suggests that at least initially it was a neutron
star). In any case, the basic idea is that when the central part of the star fuses its way to iron, it can't go any farther
because at low pressures iron 56 has the highest binding energy per nucleon of any element, so fusion or fission of iron 56
requires an energy input. Thus, the iron core just accumulates until it gets to about 1.4 solar masses (the "Chandrasekhar
mass"), at which point the electron degeneracy pressure that had been supporting it against gravity gives up the ghost and
collapses inward. At the very high pressures involved in this collapse, it is energetically favorable to combine protons and
electrons to form neutrons plus neutrinos. The neutrinos escape after scattering a bit and helping the supernova happen, and
the neutrons settle down to become a neutron star, with neutron degeneracy managing to oppose gravity. Since the supernova
rate is around 1 per 30 years, and because most supernovae probably make neutron stars instead of black holes, in the 10 billion
year lifetime of the galaxy there have probably been 10^8 to 10^9 neutron stars formed. One other way, maybe, of forming neutron
stars is to have a white dwarf accrete enough mass to push over the Chandrasekhar mass, causing a collapse. This is speculative,
though, so I won't talk about it further.
The guts of a neutron star
We'll talk about neutron star evolution in a bit, but let's say you take your run of the mill mature neutron star, which has
recovered from its birth trauma. What is its structure like? First, the typical mass of a neutron star is about 1.4 solar
masses, and the radius is probably about 10 km. By the way, the "mass" here is the gravitational mass (i.e., what you'd put
into Kepler's laws for a satellite orbiting far away). This is distinct from the baryonic mass, which is what you'd get if
you took every particle from a neutron star and weighed it on a distant scale. Because the gravitational redshift of a neutron
star is so great, the gravitational mass is about 20% lower than the baryonic mass. Anyway, imagine starting at the surface
of a neutron star and burrowing your way down. The surface gravity is about 10^11 times Earth's, and the magnetic field is
about 10^12 Gauss, which is enough to completely mess up atomic structure: for example, the ground state binding energy of
hydrogen rises to 160 eV in a 10^12 Gauss field, versus 13.6 eV in no field. In the atmosphere and upper crust, you have lots
of nuclei, so it isn't primarily neutrons yet. At the top of the crust, the nuclei are mostly iron 56 and lighter elements,
but deeper down the pressure is high enough that the equilibrium atomic weights rise, so you might find Z=40, A=120 elements
eventually. At densities of 10^6 g/cm^3 the electrons become degenerate, meaning that electrical and thermal conductivities
are huge because the electrons can travel great distances before interacting. Deeper yet, at a density around 4x10^11 g/cm^3,
you reach the "neutron drip" layer. At this layer, it becomes energetically favorable for neutrons to float out of the nuclei
and move freely around, so the neutrons "drip" out. Even further down, you mainly have free neutrons, with a 5%-10% sprinkling
of protons and electrons. As the density increases, you find what has been dubbed the "pasta-antipasta" sequence. At relatively
low (about 10^12 g/cm^3) densities, the nucleons are spread out like meatballs that are relatively far from each other. At
higher densities, the nucleons merge to form spaghetti-like strands, and at even higher densities the nucleons look like sheets
(such as lasagna). Increasing the density further brings a reversal of the above sequence, where you mainly have nucleons
but the holes form (in order of increasing density) anti-lasagna, anti-spaghetti, and anti-meatballs (also called Swiss cheese).
When the density exceeds the nuclear density 2.8x10^14 g/cm^3 by a factor of 2 or 3, really exotic stuff might be able to
form, like pion condensates, lambda hyperons, delta isobars, and quark-gluon plasmas. Here's a gorgeous figure (from www.lsw.uni-heidelberg.de/~mcamenzi/NS_Mass.html) that shows the structure of a neutron star:

Yes, you may say, that's all very well for keeping nuclear theorists employed, but how can we possibly tell if it works
out in reality? Well, believe it or not, these things may actually have an effect on the cooling history of the star and their
spin behavior! That's part of the next section.
The decline and fall of a neutron star
Thermal history
At the moment of a neutron star's birth, the nucleons that compose it have energies characteristic of free fall, which
is to say about 100 MeV per nucleon. That translates to 10^12 K or so. The star cools off very quickly, though, by neutrino
emission, so that within a couple of seconds the temperature is below 10^11 K and falling fast. In this early stage of a neutron
star's life neutrinos are produced copiously, and since if the neutrinos have energies less than about 10 MeV they sail right
through the neutron star without interacting, they act as a wonderful heat sink. Early on, the easiest way to produce neutrinos
is via the so-called "URCA" processes: n->p+e+(nu) [where (nu) means an antineutrino] and p+e->n+nu. If the core is
composed of only "ordinary" matter (neutrons, protons, and electrons), then when the temperature drops below about 10^9 K
all particles are degenerate and there are so many more neutrons than protons or electrons that the URCA processes don't conserve
momentum, so a bystander particle is required, leading to the "modified URCA" processes n+n->n+p+e+(nu) and n+p+e->n+n+nu.
The power lost from the neutron stars to neutrinos due to the modified URCA processes goes like T^8, so as the star cools
down the emission in neutrinos drops sharply. When the temperature has dropped far enough (probably between 10 and 10,000
years after the birth of the neutron star), processes less sensitive to the temperature take over. One example is standard
thermal photon cooling, which has a power proportional to T^4. Another example is thermal pair bremsstrahlung in the crust,
where an electron passes by a nucleus and, instead of emitting a single photon as in standard bremsstrahlung, emits a neutrino-antineutrino
pair. This has a power that goes like T^6, but its importance is uncertain. In any case, the qualitative picture of "standard
cooling" that has emerged is that the star first cools by URCA processes, then by modified URCA, then by neutrino pair bremsstrahlung,
then by thermal photon emission. In such a picture, a 1,000 year old neutron star (like the Crab pulsar) would have a surface
temperature of a few million degrees Kelvin. But it may not be that simple... Near the center of a neutron star, depending
on the equation of state the density can get up to several times nuclear density. This is a regime that we can't explore on
Earth, because the core temperatures of 10^9 K that are probably typical of young neutron stars are actually cold
by nuclear standards, since in accelerators when high densities are produced it's always by smashing together particles with
high Lorentz factors. Here, the thermal energies of the particles are much less than their rest masses. Anyway, that leaves
us with only theoretical predictions, which (as you might expect given the lack of data to guide us) vary a lot. Some people
think that strange matter, pion condensates, lambda hyperons, delta isobars, or free quark matter might form under those conditions,
and it seems to be a general rule that no matter what the weird stuff is, if you have exotic matter then neutrino cooling
processes proportional to T^6 can exist, which would mean that the star would cool off much faster than you thought. It even
appears possible in some equations of state that the proton and electron fraction in the core may be high enough that the
URCA process can operate, which would really cool things down in a hurry. Adding to the complication is that the neutrons
probably form a superfluid (along with the protons forming a superconductor!), and depending on the critical temperature some
of the cooling processes may get cut off. So how do we test all this? We expect that after a hundred years or so the core
will become isothermal (because it is then superfluid), and we can estimate thermal conductivities in the crust, so if we
could measure the surface temperatures of many neutron stars, then we could estimate their core temperatures, which combined
with age estimates and an assumption that all neutron stars are basically the same would tell us about their thermal evolution,
which in turn would give us a hint about whether we needed exotic matter. Unfortunately, neutron stars are so small that even
at the 10^6 K or higher temperatures expected for young neutron stars we can just barely detect them. Adding to the difficulty
is that at those temperatures the peak emission is easily absorbed by the interstellar medium, so we can only see the high-energy
tail clearly. Nonetheless, ROSAT has detected persistent X-ray emission from several young, nearby neutron stars, so now we
have to interpret this emission and decide what it tells us about the star's temperature. This ain't easy. The first complication
is that the X-ray emission might not be thermal. Instead, it could be nonthermal emission from the magnetosphere. That could
carry information of its own, but it makes temperature determinations difficult; basically, we have to say that, strictly,
we only have upper limits on the thermal emission. Even if it were all thermal, we need to remember that we only see a section
of the spectrum that is observable by an X-ray satellite, so we could be fooling ourselves about the bolometric luminosity.
In fact, some early simulations of radiation transfer through a neutron star atmosphere indicated that a neutron star of effective
temperature T_eff would yield far more observed counts than a blackbody at T_eff. Thus, a blackbody fit would overestimate
the true temperature. These simulations used opacities computed for zero magnetic field. Thus, especially for low atomic number
elements such as helium, there weren't any opacity sources at 500 eV (where the detectors operate), so in effect we would
be seeing deeper into the atmosphere where it was hotter. Such simulations may be relevant for millisecond pulsars, which
have magnetic fields in the 10^8 G to 10^10 G range. Most pulsars, though, have much stronger fields, on the order of 10^12
G. In fields this strong, the binding energies of atoms go up (as mentioned before, the ground state binding energy of hydrogen
in 10^12 G is 160 eV), meaning that the opacity at those higher energies rises as well. Thus, the X-ray detectors don't see
as far down into the atmosphere, and the inferred temperature is less than in the nonmagnetic case. The details of the magnetic
calculations are very difficult to do accurately, as they require precise computations of ionization equilibrium and polarized
radiative transfer, and these are nasty in strong fields and dense, hot, matter. It seems, though, that when magnetic effects
are included a blackbody isn't too bad an approximation. Stay tuned. So what does all this mean with respect to neutron
star composition? Yep, you guessed it, we don't have enough data.
Spin history
Neutron stars rotate very rapidly, up to 600 times per second. But how are they spinning when they are born? They may be
born rotating very fast, with periods comparable to a millisecond (although evidence is ambiguous). After that, they spin
down ever after because of magnetic torques. This seems to be supported by the fact that some of the youngest pulsars, such
as the Crab pulsar (33 ms) and the Vela pulsar (80 ms) have unusually short periods. After a pulsar is born, its magnetic
field will exert a torque and slow it down, with typical spindown rates of 10^-13 s/s for a young pulsar like the Crab. Although
overall the tendency is for isolated pulsars to slow down, they can undergo very brief periods of spinup. These events are
called "glitches", and they can momentarily change the period of a pulsar by up to a few parts in a million. The effects of
glitches decay away in a few days, and then the pulsar resumes its normal spindown. In current models of glitches, the superfluid
core and normal crust are presumed to couple impulsively, and since the crust had been spun down by the magnetic field while
the superfluid kept rotating at its original rate, this coupling would speed up the crust, leading to the observed spinup.
It is very difficult to treat this process from first (nuclear) principles, because the critical angular velocity difference
at which the crust and superfluid finally couple depends sensitively on various ill-determined properties of neutron superfluids,
and since these properties aren't directly accessible by experiments we may have to be satisfied by our current phenomenological
description. Incidentally, the glitch should also heat up the crust, and late in the lifetime of the neutron star heating
by rotational dissipation can actually become a significant source of heat and affect the temperature evolution. Fine, so
that's an isolated neutron star. If the star has a companion, it can accrete from the companion and have its rotational frequency
altered that way. If the companion is a low-mass star, say half the mass of our Sun or lower, accretion tends to proceed by
Roche lobe overflow (more on that later). This type of flow has a lot of angular momentum, so the matter forms a disk around
the star. The radius of the inner edge of the disk is determined by the strength of the magnetic field; the stronger the field,
the farther out it can control the accretion flow (for a given accretion rate). The star then (more or less) tries to come
to equilibrium with the Keplerian angular velocity of the matter at the inner edge of the accretion disk. This means that
neutron stars with relatively small (10^8 to 10^9 Gauss) magnetic fields can be spun up to high frequencies, and this is the
accepted picture of how we get millisecond pulsars. If the companion of the neutron star is a high-mass star (over 10 solar
masses) instead, then the matter that makes it onto the neutron star goes in the form of a low angular momentum wind. Therefore,
the neutron star isn't spun up to such high frequencies; in fact, some pulsars that are in high-mass systems have periods
longer than 1000 seconds. The process of wind accretion is a very complicated one, and numerical simulations of the process
push the limits of computers. It appears that, in some circumstances, a disk may form briefly around the neutron star, only
to be dissipated and replaced by a disk going the other way. One barrier to understanding this kind of accretion is that,
even with today's computers, high-resolution 3D simulations just aren't feasible now, so we have to derive what insight we
can from good two-dimensional calculations.
Misanthropic (aka isolated) neutron starsNeutrons were discovered in 1932, and very shortly afterward (in 1934) a suggestion was made by Walter Baade and Fritz Zwicky
that neutron stars were formed in supernovae. But for many decades after that, neutron stars were just hypothetical phenomena
that didn't attract much interest. Since the stars are so small, people felt that the prospects for observing them were minimal,
and thus little effort was expended on theory or observation of neutron stars. This changed dramatically in 1967, due to serendipity
and the diligence of an English graduate student by the name of Jocelyn Bell. Bell and her advisor, Anthony Hewish, were working
on radio observations of quasars, which had been discovered in 1963. Bell and some other graduate students constructed a scintillation
array for the observations, then she got down to examining the charts of data produced (she had to analyze the miles of charts
by hand, since this was in the days before powerful computers!). One day she noticed a bit of "scruff" that appeared on the
charts every second and a third. The scruff was so regular that she first thought it must be artificial. However, careful
checking showed that indeed the signal was extraterrestrial, and in fact that it must be from outside the solar system. This
source, CP 1919, was the first radio pulsar to be discovered. The discovery initiated a storm of activity that has still not
abated. A number of other pulsars were discovered, including one in the Crab Nebula, site of a famous supernova in the year
1054 that was observed by Chinese, Arabic, and North American astronomers (but not recorded, as far as we know, by Europeans).
Within a year or so of the initial discovery, it became clear that (1) pulsars are fast, with periods known in 1968 from 0.033
seconds (the Crab pulsar) to about 2 seconds, (2) the pulsations are very regular, with a typical rate of change of only a
second per ten million years, and (3) over time, the period of a pulsar always increased slightly. With this data,
it was realized quickly that pulsars had to be rotating neutron stars. With certain exceptions that don't apply in this case,
if a source varies over some time t, then its size must be less than the distance light can travel in that time,
or ct (otherwise the variation would be happening faster than the speed of light). Thus, these objects had to be
less than 300,000 km/s times 0.033 seconds, or 10,000 km, in size. This restricts us to white dwarfs, neutron stars, or black
holes. You can get a periodic signal from such objects via pulsation, rotation, or a binary orbit. White dwarfs are large
enough that their maximum pulsational, rotational, or orbital frequencies are more than a second, so this is ruled out. Black
holes don't have solid surfaces to which to attach a beacon, so rotation or vibration of black holes is eliminated. Black
holes or neutron stars in a binary could produce the required range of periods, but the binary would emit gravitational radiation,
the stars would get closer together, and the period would decrease, not increase (and would do so very quickly, too!).
Pulsations of neutron stars typically have periods of milliseconds, not seconds. The only thing left is rotating neutron stars,
and this fits all of the observations admirably. Here's an animated gif of a pulsar. There have now been more than 1000 radio pulsars discovered, with periods from about 1.6 milliseconds to more
than 5 seconds. Their discovery is considered one of the three most important astronomical discoveries in the latter half
of the twentieth century (along with quasars and the microwave background), and in part for his role in the discovery of pulsars
Anthony Hewish shared the 1974 Nobel Prize in physics.
Centauro event
A Centauro event is a kind of anomalous event observed in cosmic-ray detectors since 1972. They are so named because their shape resembles that of a centaur. If some versions of string theory are correct, then high-energy cosmic rays could create black holes when they collide with molecules in the Earth's atmosphere. These black holes would be tiny, with a mass of around 10 micrograms. They would also be unstable enough to explode in a burst of particles within around a billion-billion-billionth
of a second (10-27 of a second), these miniature black holes could explain certain anomalous observations made by
cosmic-ray detectors in the Bolivian Andes and on a mountain in Tajikistan. In 1972, the Andean detector registered a cascade that was strangely rich in charged, quark-based particles; far more particles were detected in the bottom portion of the detector than in the top portion .
It was called a "Centauro" event, because it resembled the half-man half-horse beings of Greek mythology.In years since, the detectors in Bolivia and Tajikistan have detected more than 40 Centauro events. Various explanations
have been suggested. One possible explanation might be if the strong force between particles behaves unusually when they have extremely high energies. Exploding black holes are also a possibility.
The team calculated what signal a detector would register if a cosmic ray creates a miniature black hole that explodes nearby.
The researchers' prediction is consistent with the observed Centauro events. The Tomaras team hopes that computer simulations
of mini black holes exploding, and further observations, will solve the puzzle. If they are successful it would confirm hidden
dimensions in our universe. If so, particle accelators like the one at CERN will soon be able to manufacture black holes to order and the Large Hadron Collider, scheduled to begin operations in 2007, would have enough energy to create thousands of black holes every day.
Quantum gravity is the field of theoretical physics attempting to unify the theory of quantum mechanics, which describes three of the fundamental forces of nature, with general relativity, the theory of the fourth fundamental force: gravity. The ultimate goal of some (e.g. string theory) is a unified framework for all fundamental forces—a theory of everything.
Much of the difficulty in merging these theories comes from the radically different assumptions that these theories
make on how the universe works. Quantum field theory depends on particle fields embedded in the flat space-time of special relativity. General relativity models gravity as a curvature within space-time that changes as mass moves. The most obvious ways of combining the two (such as treating gravity as simply another
particle field) run quickly into what is known as the renormalization problem. Gravity particles would attract each other and adding together all of the interactions results in many infinite
values which cannot easily be cancelled out mathematically to yield sensible, finite results. This is in contrast with quantum electrodynamics where the interactions sometimes evaluate to infinite results, but those are few enough in number to be removable
via renormalization.
Both quantum mechanics and general relativity have been highly successful. Unfortunately, the energies and conditions at which quantum gravity effects are likely
to be important are inaccessible to current laboratory experiments. The result is there are no experimental observations which
would provide any hints as to how to combine the two.
The general approach taken in deriving a theory of quantum gravity is to assume that the underlying theory will
be simple and elegant and then to look at current theories for symmetries and hints for how to combine them elegantly into
an overarching theory. One problem with this approach is that it is not known if quantum gravity will be a simple and elegant
theory.
Such a theory is required in order to understand those problems involving the combination of very large mass or
energy and very small dimensions of space, such as the behaviour of black holes, and the origin of the universe.
listening to learn

|
Space and Time Warps
This lecture is the intellectual property
of Professor S.W. Hawking. You may not reproduce, edit or distribute this document in anyway for monetary advantage.
In
science fiction, space and time warps are a commonplace. They are used for rapid journeys around the galaxy, or for travel
through time. But today's science fiction, is often tomorrow's science fact. So what are the chances for space and time warps.
The idea that space and time can be curved, or warped, is fairly recent. For more than two thousand years, the axioms
of Euclidean geometry, were considered to be self evident.  As those of you that were forced to learn Euclidean geometry at school may remember, one of the consequences of these axioms
is, that the angles of a triangle, add up to a hundred and 80 degrees. As those of you that were forced to learn Euclidean geometry at school may remember, one of the consequences of these axioms
is, that the angles of a triangle, add up to a hundred and 80 degrees.
However, in the last century, people began
to realize that other forms of geometry were possible, in which the angles of a triangle, need not add up to a hundred and
80 degrees. Consider, for example, the surface of the Earth. The nearest thing to a straight line on the surface of the Earth,
is what is called, a great circle. These are the shortest paths between two points, so they are the roots that air lines use.
Consider now the triangle on the surface of the Earth, made up of the equator, the line of 0 degrees longitude through London,
and the line of 90 degrees longtitude east, through Bangladesh.  The two lines of longitude, meet the equator at a right angle, 90 degrees. The two lines of longitude also meet each other
at the north pole, at a right angle, or 90 degrees. Thus one has a triangle with three right angles. The angles of this triangle
add up to two hundred and seventy degrees. This is greater than the hundred and eighty degrees, for a triangle on a flat surface.
If one drew a triangle on a saddle shaped surface, one would find that the angles added up to less than a hundred and eighty
degrees. The surface of the Earth, is what is called a two dimensional space. That is, you can move on the surface of the
Earth, in two directions at right angles to each other: you can move north south, or east west. But of course, there is a
third direction at right angles to these two, and that is up or down. That is to say, the surface of the Earth exists in three-dimensional
space. The three dimensional space is flat. That is to say, it obeys Euclidean geometry. The angles of a triangle, add up
to a hundred and eighty degrees. However, one could imagine a race of two dimensional creatures, who could move about on the
surface of the Earth, but who couldn't experience the third direction, of up or down. They wouldn't know about the flat three-dimensional
space, in which the surface of the Earth lives. For them, space would be curved, and geometry would be non-Euclidean. The two lines of longitude, meet the equator at a right angle, 90 degrees. The two lines of longitude also meet each other
at the north pole, at a right angle, or 90 degrees. Thus one has a triangle with three right angles. The angles of this triangle
add up to two hundred and seventy degrees. This is greater than the hundred and eighty degrees, for a triangle on a flat surface.
If one drew a triangle on a saddle shaped surface, one would find that the angles added up to less than a hundred and eighty
degrees. The surface of the Earth, is what is called a two dimensional space. That is, you can move on the surface of the
Earth, in two directions at right angles to each other: you can move north south, or east west. But of course, there is a
third direction at right angles to these two, and that is up or down. That is to say, the surface of the Earth exists in three-dimensional
space. The three dimensional space is flat. That is to say, it obeys Euclidean geometry. The angles of a triangle, add up
to a hundred and eighty degrees. However, one could imagine a race of two dimensional creatures, who could move about on the
surface of the Earth, but who couldn't experience the third direction, of up or down. They wouldn't know about the flat three-dimensional
space, in which the surface of the Earth lives. For them, space would be curved, and geometry would be non-Euclidean.
It
would be very difficult to design a living being that could exist in only two dimensions. 
Food that the creature couldn't digest would have to be spat out the same  way it came in. If there were a passage right the way through, like we have, the poor animal would fall apart. way it came in. If there were a passage right the way through, like we have, the poor animal would fall apart.
So
three dimensions, seems to be the minimum for life. But just as one can think of two dimensional beings living on the surface
of the Earth, so one could imagine that the three dimensional space in which we live, was the surface of a sphere, in another
dimension that we don't see. If the sphere were very large, space would be nearly flat, and Euclidean geometry would be a
very good approximation over small distances. But we would notice that Euclidean geometry broke down, over large distances.
As an illustration of this, imagine a team of painters, adding paint to the surface of a large ball.  As the thickness of the paint layer increased, the surface area would go up. If the ball were in a flat three-dimensional
space, one could go on adding paint indefinitely, and the ball would get bigger and bigger. However, if the three-dimensional
space, were really the surface of a sphere in another dimension, its volume would be large but finite. As one added more layers
of paint, the ball would eventually fill half the space. After that, the painters would find that they were trapped in a region
of ever decreasing size, and almost the whole of space, was occupied by the ball, and its layers of paint. So they would know
that they were living in a curved space, and not a flat one As the thickness of the paint layer increased, the surface area would go up. If the ball were in a flat three-dimensional
space, one could go on adding paint indefinitely, and the ball would get bigger and bigger. However, if the three-dimensional
space, were really the surface of a sphere in another dimension, its volume would be large but finite. As one added more layers
of paint, the ball would eventually fill half the space. After that, the painters would find that they were trapped in a region
of ever decreasing size, and almost the whole of space, was occupied by the ball, and its layers of paint. So they would know
that they were living in a curved space, and not a flat one | General Relativity was a major
intellectual revolution that has transformed the way we think about the universe. It is a theory not only of curved space,
but of curved or warped time as well. Einstein had realized in 1905, that space and time, are intimately connected with each
other. One can describe the location of an event by four numbers. Three numbers describe the position of the event. They could
be miles north and east of Oxford circus, and height above sea level. On a larger scale, they could be galactic latitude and
longitude, and distance from the center of the galaxy. The fourth number, is the time of the event. Thus one can think of
space and time together, as a four-dimensional entity, called space-time. Each point of space-time is labeled by four numbers,
that specify its position in space, and in time. Combining space and time into space-time in this way would be rather trivial,
if one could disentangle them in a unique way. That is to say, if there was a unique way of defining the time and position
of each event. However, in a remarkable paper written in 1905, when he was a clerk in the Swiss patent office, Einstein showed
that the time and position at which one thought an event occurred, depended on how one was moving. This meant that time and
space, were inextricably bound up with each other. The times that different observers would assign to events would agree if
the observers were not moving relative to each other. But they would disagree more, the faster their relative speed. So one
can ask, how fast does one need to go, in order that the time for one observer, should go backwards relative to the time of
another observer. The answer is given in the following Limerick. There was a young lady of Wight, Who traveled
much faster than light, She departed one day, In a relative way, And arrived on the previous night. So all
we need for time travel, is a space ship that will go faster than light. Unfortunately, in the same paper, Einstein showed
that the rocket power needed to accelerate a space ship, got greater and greater, the nearer it got to the speed of light.
So it would take an infinite amount of power, to accelerate past the speed of light. Einstein's paper of 1905 seemed
to rule out time travel into the past. It also indicated that space travel to other stars, was going to be a very slow and
tedious business. If one couldn't go faster than light, the round trip to the nearest star, would take at least eight years,
and to the center of the galaxy, at least eighty thousand years. If the space ship went very near the speed of light, it might
seem to the people on board, that the trip to the galactic center had taken only a few years. But that wouldn't be much consolation,
if everyone you had known was dead and forgotten thousands of years ago, when you got back. That wouldn't be much good for
space Westerns. So writers of science fiction, had to look for ways to get round this difficulty. In his 1915 paper,
Einstein showed that the effects of gravity could be described, by supposing that space-time was warped or distorted, by the
matter and energy in it. We can actually observe this warping of space-time, produced by the mass of the Sun, in the slight
bending of light or radio waves, passing close to the Sun.  This causes the apparent position of the star or radio source, to shift slightly, when the Sun is between the Earth and the
source. The shift is very small, about a thousandth of a degree, equivalent to a movement of an inch, at a distance of a mile.
Nevertheless, it can be measured with great accuracy, and it agrees with the predictions of General Relativity. We have experimental
evidence, that space and time are warped. The amount of warping in our neighbourhood, is very small, because all the gravitational
fields in the solar system, are weak. However, we know that very strong fields can occur, for example in the Big Bang, or
in black holes. So, can space and time be warped enough, to meet the demands from science fiction, for things like hyper space
drives, wormholes, or time travel. At first sight, all these seem possible. For example, in 1948, Kurt Goedel found a solution
of the field equations of General Relativity, which represents a universe in which all the matter was rotating. In this universe,
it would be possible to go off in a space ship, and come back before you set out. Goedel was at the Institute of Advanced
Study, in Princeton, where Einstein also spent his last years. He was more famous for proving you couldn't prove everything
that is true, even in such an apparently simple subject as arithmetic. But what he proved about General Relativity allowing
time travel really upset Einstein, who had thought it wouldn't be possible. We now know that Goedel's solution couldn't
represent the universe in which we live, because it was not expanding. It also had a fairly large value for a quantity called
the cosmological constant, which is generally believed to be zero. However, other apparently more reasonable solutions that
allow time travel, have since been found. A particularly interesting one contains two cosmic strings, moving past each other
at a speed very near to, but slightly less than, the speed of light.  Cosmic strings are a remarkable idea of theoretical physics, which science fiction writers don't really seem to have caught
on to. As their name suggests, they are like string, in that they have length, but a tiny cross section. Actually, they are
more like rubber bands, because they are under enormous tension, something like a hundred billion billion billion tons. A
cosmic string attached to the Sun would accelerate it naught to sixty, in a thirtieth of a second. Cosmic strings
may sound far-fetched, and pure science fiction, but there are good scientific reasons to believed they could have formed
in the very early universe, shortly after the Big Bang. Because they are under such great tension, one might have expected
them to accelerate to almost the speed of light. What both the Goedel universe, and the fast moving cosmic string space-time
have in common, is that they start out so distorted and curved, that travel into the past, was always possible. God might
have created such a warped universe, but we have no reason to think that He did. All the evidence is, that the universe started
out in the Big Bang, without the kind of warping needed, to allow travel into the past. Since we can't change the way the
universe began, the question of whether time travel is possible, is one of whether we can subsequently make space-time so
warped, that one can go back to the past. I think this is an important subject for research, but one has to be careful not
to be labeled a crank. If one made a research grant application to work on time travel, it would be dismissed immediately.
No government agency could afford to be seen to be spending public money, on anything as way out as time travel. Instead,
one has to use technical terms, like closed time like curves, which are code for time travel. Although this lecture is partly
about time travel, I felt I had to give it the scientifically more respectable title, Space and Time warps. Yet, it is a very
serious question. Since General Relativity can permit time travel, does it allow it in our universe? And if not, why not.
Closely related to time travel, is the ability to travel rapidly from one position in space, to another. As I said
earlier, Einstein showed that it would take an infinite amount of rocket power, to accelerate a space ship to beyond the speed
of light. So the only way to get from one side of the galaxy to the other, in a reasonable time, would seem to be if we could
warp space-time so much, that we created a little tube or wormhole.  This could connect the two sides of the galaxy, and act as a short cut, to get from one to the other and back while your
friends were still alive. Such wormholes have been seriously suggested, as being within the capabilities of a future civilization.
But if you can travel from one side of the galaxy, to the other, in a week or two, you could go back through another wormhole,
and arrive back before you set out. You could even manage to travel back in time with a single wormhole, if its two ends were
moving relative to each other.  One can show that to create a wormhole, one needs to warp space-time in the opposite way, to that in which normal matter warps
it. Ordinary matter curves space-time back on itself, like the surface of the Earth. However, to create a wormhole,
one needs matter that warps space-time in the opposite way, like the surface of a saddle. The same is true of any other way
of warping space-time to allow travel to the past, if the universe didn't begin so warped, that it allowed time travel. What
one would need, would be matter with negative mass, and negative energy density, to make space-time warp in the way required. Energy
is rather like money. If you have a positive bank balance, you can distribute it in various ways. But according to the classical
laws that were believed until quite recently, you weren't allowed to have an energy overdraft. So these classical laws would
have ruled out us being able to warp the universe, in the way required to allow time travel. However, the classical laws were
overthrown by Quantum Theory, which is the other great revolution in our picture of the universe, apart from General Relativity.
Quantum Theory is more relaxed, and allows you to have an overdraft on one or two accounts. If only the banks were as accommodating.
In other words, Quantum Theory allows the energy density to be negative in some places, provided it is positive in others.
The reason Quantum Theory can allow the energy density to be negative, is that it is based on the Uncertainty Principle.
 This says that certain quantities, like the position and speed of a particle, can't both have well defined
values. The more accurately the position of a particle is defined, the greater is the uncertainty in its speed, and vice versa.
The uncertainty principle also applies to fields, like the electro-magnetic field, or the gravitational field. It implies
that these fields can't be exactly zeroed, even in what we think of as empty space. For if they were exactly zero, their values
would have both a well-defined position at zero, and a well-defined speed, which was also zero. This would be a violation
of the uncertainty principle. Instead, the fields would have to have a certain minimum amount of fluctuations. One can interpret
these so called vacuum fluctuations, as pairs of particles and anti particles, that suddenly appear together, move apart,
and then come back together again, and annihilate each other.  These particle anti particle pairs, are said to be virtual, because one can not measure them directly with a particle detector.
However, one can observe their effects indirectly. One way of doing this, is by what is called the Casimir effect. One has
two parallel metal plates, a short distance apart. The plates act like mirrors for the virtual particles and anti particles.
This means that the region between the plates, is a bit like an organ pipe, and will only admit light waves of certain resonant
frequencies. The result is that there are slightly fewer vacuum fluctuations, or virtual particles, between the plates, than
outside them, where vacuum fluctuations can have any wavelength. The reduction in the number of virtual particles between
the plates means that they don't hit the plates so often, and thus don't exert as much pressure on the plates, as the virtual
particles outside. There is thus a slight force pushing the plates together. This force has been measured experimentally.
So virtual particles actually exist, and produce real effects. Because there are fewer virtual particles, or vacuum fluctuations,
between the plates, they have a lower energy density, than in the region outside. But the energy density of empty space far
away from the plates, must be zero. Otherwise it would warp space-time, and the universe wouldn't be nearly flat. So the energy
density in the region between the plates, must be negative. We thus have experimental evidence from the bending of
light, that space-time is curved, and confirmation from the Casimir effect, that we can warp it in the negative direction.
So it might seem possible, that as we advance in science and technology, we might be able to construct a wormhole, or warp
space and time in some other way, so as to be able to travel into our past. If this were the case, it would raise a whole
host of questions and problems. One of these is, if sometime in the future, we learn to travel in time, why hasn't someone
come back from the future, to tell us how to do it.  Even if there were sound reasons for keeping us in ignorance, human nature being what it is, it is difficult to believe that
someone wouldn't show off, and tell us poor benighted peasants, the secret of time travel. Of course, some people would claim
that we have been visited from the future. They would say that UFO's come from the future, and that governments are engaged
in a gigantic conspiracy to cover them up, and keep for themselves, the scientific knowledge that these visitors bring. All
I can say is, that if governments were hiding something, they are doing a pretty poor job, of extracting useful information
from the aliens. I'm pretty skeptical of conspiracy theories, believing the cock up theory is more likely. The reports of
sightings of UFO's can't all be caused by extra terrestrials, because they are mutually contradictory. But once you admit
that some are mistakes, or hallucinations, isn't it more probable that they all are, than that we are being visited by people
from the future, or the other side of the galaxy? If they really want to colonize the Earth, or warn us of some danger, they
are being pretty ineffective. A possible way to reconcile time travel, with the fact that we don't seem to have had any
visitors from the future, would be to say that it can occur only in the future. In this view, one would say space-time in
our past was fixed, because we have observed it, and seen that it is not warped enough, to allow travel into the past. On
the other hand, the future is open. So we might be able to warp it enough, to allow time travel. But because we can warp space-time
only in the future, we wouldn't be able to travel back to the present time, or earlier.  This picture would explain why we haven't been over run by tourists from the future.  But it would still leave plenty of paradoxes. Suppose it were possible to go off in a rocket ship, and come back before you
set off. What would stop you blowing up the rocket on its launch pad, or otherwise preventing you from setting out in the
first place. There are other versions of this paradox, like going back, and killing your parents before you were born, but
they are essentially equivalent. There seem to be two possible resolutions.  One is what I shall call, the consistent histories approach. It says that one has to find a consistent
solution of the equations of physics, even if space-time is so warped, that it is possible to travel into the past. On this
view, you couldn't set out on the rocket ship to travel into the past, unless you had already come back, and failed to blow
up the launch pad. It is a consistent picture, but it would imply that we were completely determined: we couldn't change our
minds. So much for free will. The other possibility is what I call, the alternative histories approach. It has been championed
by the physicist David Deutsch, and it seems to have been what Stephen Spielberg had in mind when he filmed, Back to the Future.
In this view, in one alternative history,  there would not have been any return from the future, before the rocket set off, and so no possibility of it being blown up.
But when the traveler returns from the future, he enters another alternative history. In this, the human race makes a tremendous
effort to build a space ship, but just before it is due to be launched, a similar space ship appears from the other side of
the galaxy, and destroys it. David Deutsch claims support for the alternative histories approach, from the sum over histories
concept, introduced by the physicist, Richard Feinman, who died a few years ago. The idea is that according to Quantum Theory,
the universe doesn't have just a unique single history.  Instead, the universe has every single possible history,each with its own probability. There must be a possible history in
which there is a lasting peace in the Middle East, though maybe the probability is low. In some histories space-time will
be so warped, that objects like rockets will be able to travel into their pasts. But each history is complete and self contained,
describing not only the curved space-time, but also the objects in it. So a rocket can not transfer to another alternative
history, when it comes round again. It is still in the same history, which has to be self consistent. Thus, despite what Deutsch
claims, I think the sum over histories idea, supports the consistent histories hypothesis, rather than the alternative histories
idea. It thus seems that we are stuck with the consistent histories picture. However, this need not involve problems
with determinism or free will, if the probabilities are very small, for histories in which space-time is so warped, that time
travel is possible over a macroscopic region. This is what I call, the Chronology Protection Conjecture: the laws of physics
conspire to prevent time travel, on a macroscopic scale. It seems that what happens, is that when space-time gets
warped almost enough to allow travel into the past, virtual particles can almost become real particles, following closed trajectories.
The density of the virtual particles, and their energy, become very large. This means that the probability of these histories
is very low. Thus it seems there may be a Chronology Protection Agency at work, making the world safe for historians. But
this subject of space and time warps is still in its infancy. According to string theory, which is our best hope of uniting
General Relativity and Quantum Theory, into a Theory of Everything, space-time ought to have ten dimensions, not just the
four that we experience. The idea is that six of these ten dimensions are curled up into a space so small, that we don't notice
them. On the other hand, the remaining four directions are fairly flat, and are what we call space-time. If this picture is
correct, it might be possible to arrange that the four flat directions got mixed up with the six highly curved or warped directions.
What this would give rise to, we don't yet know. But it opens exciting possibilities. The conclusion of this lecture
is that rapid space-travel, or travel back in time, can't be ruled out, according to our present understanding. They would
cause great logical problems, so let's hope there's a Chronology Protection Law, to prevent people going back, and killing
our parents. But science fiction fans need not lose heart. There's hope in string theory. Since we haven't cracked
time travel yet, I have run out of time.

1974 discovery photograph of a possible charmed baryon, now identified as the Σ c++ In particle physics, the quarks are subatomic particles thought to be elemental and indivisible. They are one of the two kinds of spin-½ fermions (the other being the leptons). Objects made up of quarks are known as hadrons; well known examples are protons and neutrons. Quarks are generally believed to never exist alone but only in color-neutral groups of two or three (and possibly five or more); all searches for free quarks since 1977 have yielded negative results. Quarks are differentiated from leptons, the other family of fermions, by color charge. In addition, leptons (such as the electron, the muon, and the neutrino) have integral electric charge (−1 or 0 in units of the proton charge) while quarks have fractional electric charge
(+⅔ or −⅓; antiquarks have charge −⅔ or +⅓ and antileptons have charge +1 or 0).
holo-linx
For brochures or company literature:
tell us what you know!!!
|






 As those of you that were forced to learn Euclidean geometry at school may remember, one of the consequences of these axioms
is, that the angles of a triangle, add up to a hundred and 80 degrees.
As those of you that were forced to learn Euclidean geometry at school may remember, one of the consequences of these axioms
is, that the angles of a triangle, add up to a hundred and 80 degrees.  The two lines of longitude, meet the equator at a right angle, 90 degrees. The two lines of longitude also meet each other
at the north pole, at a right angle, or 90 degrees. Thus one has a triangle with three right angles. The angles of this triangle
add up to two hundred and seventy degrees. This is greater than the hundred and eighty degrees, for a triangle on a flat surface.
If one drew a triangle on a saddle shaped surface, one would find that the angles added up to less than a hundred and eighty
degrees. The surface of the Earth, is what is called a two dimensional space. That is, you can move on the surface of the
Earth, in two directions at right angles to each other: you can move north south, or east west. But of course, there is a
third direction at right angles to these two, and that is up or down. That is to say, the surface of the Earth exists in three-dimensional
space. The three dimensional space is flat. That is to say, it obeys Euclidean geometry. The angles of a triangle, add up
to a hundred and eighty degrees. However, one could imagine a race of two dimensional creatures, who could move about on the
surface of the Earth, but who couldn't experience the third direction, of up or down. They wouldn't know about the flat three-dimensional
space, in which the surface of the Earth lives. For them, space would be curved, and geometry would be non-Euclidean.
The two lines of longitude, meet the equator at a right angle, 90 degrees. The two lines of longitude also meet each other
at the north pole, at a right angle, or 90 degrees. Thus one has a triangle with three right angles. The angles of this triangle
add up to two hundred and seventy degrees. This is greater than the hundred and eighty degrees, for a triangle on a flat surface.
If one drew a triangle on a saddle shaped surface, one would find that the angles added up to less than a hundred and eighty
degrees. The surface of the Earth, is what is called a two dimensional space. That is, you can move on the surface of the
Earth, in two directions at right angles to each other: you can move north south, or east west. But of course, there is a
third direction at right angles to these two, and that is up or down. That is to say, the surface of the Earth exists in three-dimensional
space. The three dimensional space is flat. That is to say, it obeys Euclidean geometry. The angles of a triangle, add up
to a hundred and eighty degrees. However, one could imagine a race of two dimensional creatures, who could move about on the
surface of the Earth, but who couldn't experience the third direction, of up or down. They wouldn't know about the flat three-dimensional
space, in which the surface of the Earth lives. For them, space would be curved, and geometry would be non-Euclidean. 
 way it came in. If there were a passage right the way through, like we have, the poor animal would fall apart.
way it came in. If there were a passage right the way through, like we have, the poor animal would fall apart.  As the thickness of the paint layer increased, the surface area would go up. If the ball were in a flat three-dimensional
space, one could go on adding paint indefinitely, and the ball would get bigger and bigger. However, if the three-dimensional
space, were really the surface of a sphere in another dimension, its volume would be large but finite. As one added more layers
of paint, the ball would eventually fill half the space. After that, the painters would find that they were trapped in a region
of ever decreasing size, and almost the whole of space, was occupied by the ball, and its layers of paint. So they would know
that they were living in a curved space, and not a flat one
As the thickness of the paint layer increased, the surface area would go up. If the ball were in a flat three-dimensional
space, one could go on adding paint indefinitely, and the ball would get bigger and bigger. However, if the three-dimensional
space, were really the surface of a sphere in another dimension, its volume would be large but finite. As one added more layers
of paint, the ball would eventually fill half the space. After that, the painters would find that they were trapped in a region
of ever decreasing size, and almost the whole of space, was occupied by the ball, and its layers of paint. So they would know
that they were living in a curved space, and not a flat one This causes the apparent position of the star or radio source, to shift slightly, when the Sun is between the Earth and the
source. The shift is very small, about a thousandth of a degree, equivalent to a movement of an inch, at a distance of a mile.
Nevertheless, it can be measured with great accuracy, and it agrees with the predictions of General Relativity. We have experimental
evidence, that space and time are warped.
This causes the apparent position of the star or radio source, to shift slightly, when the Sun is between the Earth and the
source. The shift is very small, about a thousandth of a degree, equivalent to a movement of an inch, at a distance of a mile.
Nevertheless, it can be measured with great accuracy, and it agrees with the predictions of General Relativity. We have experimental
evidence, that space and time are warped. Cosmic strings are a remarkable idea of theoretical physics, which science fiction writers don't really seem to have caught
on to. As their name suggests, they are like string, in that they have length, but a tiny cross section. Actually, they are
more like rubber bands, because they are under enormous tension, something like a hundred billion billion billion tons. A
cosmic string attached to the Sun would accelerate it naught to sixty, in a thirtieth of a second.
Cosmic strings are a remarkable idea of theoretical physics, which science fiction writers don't really seem to have caught
on to. As their name suggests, they are like string, in that they have length, but a tiny cross section. Actually, they are
more like rubber bands, because they are under enormous tension, something like a hundred billion billion billion tons. A
cosmic string attached to the Sun would accelerate it naught to sixty, in a thirtieth of a second.  This could connect the two sides of the galaxy, and act as a short cut, to get from one to the other and back while your
friends were still alive. Such wormholes have been seriously suggested, as being within the capabilities of a future civilization.
But if you can travel from one side of the galaxy, to the other, in a week or two, you could go back through another wormhole,
and arrive back before you set out. You could even manage to travel back in time with a single wormhole, if its two ends were
moving relative to each other.
This could connect the two sides of the galaxy, and act as a short cut, to get from one to the other and back while your
friends were still alive. Such wormholes have been seriously suggested, as being within the capabilities of a future civilization.
But if you can travel from one side of the galaxy, to the other, in a week or two, you could go back through another wormhole,
and arrive back before you set out. You could even manage to travel back in time with a single wormhole, if its two ends were
moving relative to each other.  One can show that to create a wormhole, one needs to warp space-time in the opposite way, to that in which normal matter warps
it. Ordinary matter curves space-time back on itself, like the surface of the Earth.
One can show that to create a wormhole, one needs to warp space-time in the opposite way, to that in which normal matter warps
it. Ordinary matter curves space-time back on itself, like the surface of the Earth. 
 These particle anti particle pairs, are said to be virtual, because one can not measure them directly with a particle detector.
However, one can observe their effects indirectly. One way of doing this, is by what is called the Casimir effect. One has
two parallel metal plates, a short distance apart. The plates act like mirrors for the virtual particles and anti particles.
This means that the region between the plates, is a bit like an organ pipe, and will only admit light waves of certain resonant
frequencies. The result is that there are slightly fewer vacuum fluctuations, or virtual particles, between the plates, than
outside them, where vacuum fluctuations can have any wavelength. The reduction in the number of virtual particles between
the plates means that they don't hit the plates so often, and thus don't exert as much pressure on the plates, as the virtual
particles outside. There is thus a slight force pushing the plates together. This force has been measured experimentally.
So virtual particles actually exist, and produce real effects.
These particle anti particle pairs, are said to be virtual, because one can not measure them directly with a particle detector.
However, one can observe their effects indirectly. One way of doing this, is by what is called the Casimir effect. One has
two parallel metal plates, a short distance apart. The plates act like mirrors for the virtual particles and anti particles.
This means that the region between the plates, is a bit like an organ pipe, and will only admit light waves of certain resonant
frequencies. The result is that there are slightly fewer vacuum fluctuations, or virtual particles, between the plates, than
outside them, where vacuum fluctuations can have any wavelength. The reduction in the number of virtual particles between
the plates means that they don't hit the plates so often, and thus don't exert as much pressure on the plates, as the virtual
particles outside. There is thus a slight force pushing the plates together. This force has been measured experimentally.
So virtual particles actually exist, and produce real effects. Even if there were sound reasons for keeping us in ignorance, human nature being what it is, it is difficult to believe that
someone wouldn't show off, and tell us poor benighted peasants, the secret of time travel. Of course, some people would claim
that we have been visited from the future. They would say that UFO's come from the future, and that governments are engaged
in a gigantic conspiracy to cover them up, and keep for themselves, the scientific knowledge that these visitors bring. All
I can say is, that if governments were hiding something, they are doing a pretty poor job, of extracting useful information
from the aliens. I'm pretty skeptical of conspiracy theories, believing the cock up theory is more likely. The reports of
sightings of UFO's can't all be caused by extra terrestrials, because they are mutually contradictory. But once you admit
that some are mistakes, or hallucinations, isn't it more probable that they all are, than that we are being visited by people
from the future, or the other side of the galaxy? If they really want to colonize the Earth, or warn us of some danger, they
are being pretty ineffective.
Even if there were sound reasons for keeping us in ignorance, human nature being what it is, it is difficult to believe that
someone wouldn't show off, and tell us poor benighted peasants, the secret of time travel. Of course, some people would claim
that we have been visited from the future. They would say that UFO's come from the future, and that governments are engaged
in a gigantic conspiracy to cover them up, and keep for themselves, the scientific knowledge that these visitors bring. All
I can say is, that if governments were hiding something, they are doing a pretty poor job, of extracting useful information
from the aliens. I'm pretty skeptical of conspiracy theories, believing the cock up theory is more likely. The reports of
sightings of UFO's can't all be caused by extra terrestrials, because they are mutually contradictory. But once you admit
that some are mistakes, or hallucinations, isn't it more probable that they all are, than that we are being visited by people
from the future, or the other side of the galaxy? If they really want to colonize the Earth, or warn us of some danger, they
are being pretty ineffective. This picture would explain why we haven't been over run by tourists from the future.
This picture would explain why we haven't been over run by tourists from the future.  But it would still leave plenty of paradoxes. Suppose it were possible to go off in a rocket ship, and come back before you
set off. What would stop you blowing up the rocket on its launch pad, or otherwise preventing you from setting out in the
first place. There are other versions of this paradox, like going back, and killing your parents before you were born, but
they are essentially equivalent. There seem to be two possible resolutions.
But it would still leave plenty of paradoxes. Suppose it were possible to go off in a rocket ship, and come back before you
set off. What would stop you blowing up the rocket on its launch pad, or otherwise preventing you from setting out in the
first place. There are other versions of this paradox, like going back, and killing your parents before you were born, but
they are essentially equivalent. There seem to be two possible resolutions. 
 there would not have been any return from the future, before the rocket set off, and so no possibility of it being blown up.
But when the traveler returns from the future, he enters another alternative history. In this, the human race makes a tremendous
effort to build a space ship, but just before it is due to be launched, a similar space ship appears from the other side of
the galaxy, and destroys it.
there would not have been any return from the future, before the rocket set off, and so no possibility of it being blown up.
But when the traveler returns from the future, he enters another alternative history. In this, the human race makes a tremendous
effort to build a space ship, but just before it is due to be launched, a similar space ship appears from the other side of
the galaxy, and destroys it. Instead, the universe has every single possible history,each with its own probability. There must be a possible history in
which there is a lasting peace in the Middle East, though maybe the probability is low.
Instead, the universe has every single possible history,each with its own probability. There must be a possible history in
which there is a lasting peace in the Middle East, though maybe the probability is low.





 Imagine trekking in a lunar rover across miles of the Moon's rough surface. Your mission: to explore a crater with suspected
deposits of ice.
Imagine trekking in a lunar rover across miles of the Moon's rough surface. Your mission: to explore a crater with suspected
deposits of ice.  The Vision for Space Exploration calls for human and robotic missions to the Moon, Mars and beyond. To realize these ambitious
goals, we will need more powerful and efficient propulsion and power-generation systems -- systems that can thrust a spacecraft
out of Earth's orbit to the far reaches of the Universe.
The Vision for Space Exploration calls for human and robotic missions to the Moon, Mars and beyond. To realize these ambitious
goals, we will need more powerful and efficient propulsion and power-generation systems -- systems that can thrust a spacecraft
out of Earth's orbit to the far reaches of the Universe.